Numeric computing is very difficult to do properly. Richard Harris looks at whether a common technique will help.
In the first article in this series we explored floating point arithmetic and its various modes of failure. We saw that rounding error, although often touted as the big problem with floating point arithmetic, isn't really much to be concerned about when compared to cancellation error; the catastrophic loss of precision that occurs when subtracting two nearly equal floating point numbers. Finally, we noted the rather surprising fact that the order of execution of mathematical operations will result in different accumulated rounding errors and that, if we wish our calculations to be as accurate is possible, we need to carefully consider how we construct them.
In this article we shall explore the most frequently proposed alternative to it: fixed point arithmetic.
Fixed point
Fixed point arithmetic is perhaps the simplest alternative to floating point. Fixed point numbers maintain a fixed number of decimal places, rather than digits of precision. Typically they are implemented as an integer with the assumption that some constant number of the least significant base 10 digits fall below the decimal point.
For example, using a long and assuming that the last 2 decimal digits lie below the decimal point, we would represent π as 314.
Listing 1 provides an implementation of a base 10 fixed point number class.
template<class T, size_t N>
class fixed
{
public:
enum{places=N};
typedef T data_type;
fixed();
fixed(const data_type &x);
fixed(const data_type &before,
const data_type &after);
static const data_type & scale();
const data_type & data() const
int compare(const fixed &x) const;
fixed & negate();
fixed & operator+=(const fixed &x);
fixed & operator-=(const fixed &x);
fixed & operator*=(const fixed &x);
fixed & operator/=(const fixed &x);
private:
static data_type calc_scale();
data_type x_;
};
|
| Listing 1 |
This class uses the type T to represent the fixed point number, with N decimal digits after the decimal point. Note that we shall not presume that there is a specialisation of std::numeric_limits for T and hence if there isn't enough room in the type T to fit the digits we shall have undefined behaviour rather than a compilation error.
Note that, given in-place arithmetic operations and a copy constructor, it is trivial to implement the free standing arithmetic operations. Those who would prefer to avoid the computational expense of the copy could instead use member data access functions to implement more efficient free functions.
It shall henceforth be assumed that such free functions have been implemented.
The scale method is a static helper that calculates the scaling factor which we need to divide an integer by to recover the required number of decimal places, illustrated in listing 2 together with the calc_scale helper function that actually calculates it and the data member access function.
template<class T, size_t N>
const fixed<T, N>::data_type &
fixed<T, N>::scale()
{
static const data_type result = calc_scale();
return result;
}
template<class T, size_t N>
fixed<T, N>::data_type
fixed<T, N>::calc_scale()
{
data_type result(1);
for(size_t i=0;i!=places;++i)
result *= data_type(10);
return result;
}
template<class T, size_t N>
const fixed<T, N>::data_type &
fixed<T, N>::data() const
{
return x_;
}
|
| Listing 2 |
Listing 3 illustrates the constructors of this class.
Note that the only error check we're making is that the number passed to represent the digits after the decimal point in the final constructor is within the valid range; we treat overflow as undefined behaviour to keep things simple.
template<class T, size_t N>
fixed<T, N>::fixed()
{
}
template<class T, size_t N>
fixed<T, N>::fixed(const data_type &x)
: x_(x*scale())
{
}
template<class T, size_t N>
fixed<T, N>::fixed(const data_type &before,
const data_type &after)
: x_(before*scale()+after)
{
if(after<0 || after>=scale())
throw std::invalid_argument("");
}
|
| Listing 3 |
We allow implicit conversion from the underlying type to make using integers in fixed point calculations slightly easier. We do not provide any conversion between fixed and floating point numbers since this would rather defeat the purpose of using fixed point numbers in the first place.
The compare and negate member functions are provided to simplify the implementation of non-member relational and negation operators and their definitions are given in listing 4.
template<class T, size_t N>
int
fixed<T, N>::compare(const fixed &x) const
{
if(x_<x.x_) return -1;
if(x_>x.x_) return 1;
return 0;
}
template<class T, size_t N>
fixed<T, N> &
fixed<T, N>::negate()
{
x_ = -x_;
return *this;
}
|
| Listing 4 |
Addition and subtraction are straightforward operations for fixed point numbers. Since both arguments are guaranteed to have the same number of digits after the decimal point, we simply use the corresponding integer operations on the underlying type, as shown in listing 5.
template<class T, size_t N>
fixed<T, N> &
fixed<T, N>::operator+=(const fixed &x)
{
x_ += x.x_;
return *this;
}
template<class T, size_t N>
fixed<T, N> &
fixed<T, N>::operator-=(const fixed &x)
{
x_ -= x.x_;
return *this;
}
|
| Listing 5 |
Note that whilst we are again treating overflow as undefined behaviour, these operations introduce no further error into the result above and beyond those that were in their arguments.
The naïve approach to multiplication is to multiply the underlying integer values and then divide by the scaling factor since
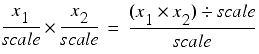
Similarly, for division we have
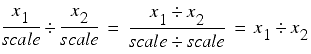
There are two problems with this approach. The first is that we are no longer rounding the result, we are merely truncating it. Without careful analysis it is possible that multiplicative operations will introduce twice as much error than they would if we had correctly rounded the result.
Fortunately, this problem is relatively easily fixed. For multiplication, we simply add half the scale before dividing by it. For division we add half of the number by which we are dividing before the actual division. Listing 6 illustrates the correctly rounded multiplication and division operators.
template<class T, size_t N>
fixed<T, N> &
fixed<T, N>::operator*=(const fixed &x)
{
x_ *= x.x_;
x_ += scale()/2;
x_ /= scale();
return *this;
}
template<class T, size_t N>
fixed<T, N> &
fixed<T, N>::operator/=(const fixed &x)
{
x_ += x.x_/2;
x_ *= scale();
x_ /= x.x_;
return *this;
}
|
| Listing 6 |
The second, and far worse, problem is that if we have a large number of digits after the decimal point, and consequently a large scaling factor, then multiplication and division are very likely to overflow the internal integer operations even for numbers close to 1.
Fixing this problem is a little trickier. What we really need is a larger integer type to store intermediate values. However, since we aren't forcing the user to use built in integers, it's not at all obvious how we should go about this, short of implementing one in terms of the internal integer type.
Because of this, I shall stick with this implementation and declare caveat emptor for users who desire a large number of digits after the decimal point.
The advantages of fixed point
So now we know exactly how to implement fixed point numbers we should probably ask ourselves why we should want to.
Well, there are three principal advantages to fixed point numbers.
The first, and by far the least important, advantage is that unlike IEEE 754-1985 floating point, it can exactly represent decimal fractions. This is trotted out ad nauseum as a reason to use fixed point but, given that a revision of the standard describes the implementation of base 10 floating point numbers, it isn't particularly compelling.
The second, slightly more important, advantage is that fixed point arithmetic can be dramatically faster on some processors.
The third, and by far the most important, advantage is that, as described above, addition and subtraction introduce no error beyond that in their arguments. This means that it is much easier to reason about addition using fixed point arithmetic; if we are summing numbers that can be exactly represented we have no rounding issues at all and need only worry about overflow.
This, together with the ability to represent some decimal fractions exactly is why many financial transactions are mandated to use base 10 fixed point numbers.
The disadvantages of fixed point
Unfortunately, multiplication is rather more problematic.
Even assuming we are not much affected by overflow of the underlying type, if we multiply fixed point numbers our calculations may be severely affected by execution order. To demonstrate just how severely, let us now assume that we are using 2 decimal place base 10 fixed point numbers to calculate the value of the expression
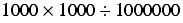
If we calculate this in the order
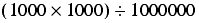
we trivially have a result of 1.
However, if we calculate it in the order
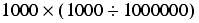
we trivially have a result of 0.
I'm sure you'll agree that this is a fairly significant difference; if you don't, multiply the whole expression by a few million for effect. The problem is that multiplicative errors accumulate proportionally rather than absolutely. Additively, fixed point numbers behave themselves but the instant we start multiplying and dividing they turn on us.
For general purpose arithmetic, therefore, fixed point numbers seem to be something of a lame duck.
Quack.
Arbitrary precision
One way to fix the problem of overflow in fixed point numbers is to use arbitrary precision integers, also known as bignums, as the underlying type.
These are typically implemented using an array of integers which can grow as needed to represent any given integer.
Listing 7 provides an implementation of an arbitrary precision integer class.
Note that we represent our number with a vector of unsigned short s and an enum to indicate the sign. For the sake of simplicity, we shall assume that short s are exactly 16 bits wide and that long s are exactly 32 bits wide. Whilst many platforms conform to these assumptions, they are not mandated by the C++ standard. A robust implementation would therefore need to take a more cautious approach.
class bignum
{
public:
typedef unsigned short digit_type;
typedef unsigned long product_type;
typedef std::vector<digit_type> data_type;
enum sign_type{
positive=1,
negative=-1
};
enum {mask=0xffff, shift=16};
bignum();
bignum(short x);
bignum(unsigned short x);
bignum(long x);
bignum(unsigned long x);
bignum(sign_type s, const data_type &x);
sign_type sign() const;
const data_type & magnitude() const;
void swap(bignum &x);
int compare(const bignum &x) const;
bignum & negate();
bignum & operator+=(const bignum &x);
bignum & operator-=(const bignum &x);
bignum & operator*=(const bignum &x);
bignum & operator/=(const bignum &x);
private:
sign_type s_;
data_type x_;
};
|
| Listing 7 |
Our underlying representation will not admit leading zeros, except for the number zero which shall consist of a single zero digit. To that end we shall require a helper function to strip leading zeros in those circumstances that we may need to; its implementation is given in listing 8.
void
data_strip_leading_zeros(bignum::data_type &x)
{
bignum::data_type::reverse_iterator first =
x.rbegin();
bignum::data_type::reverse_iterator last =
x.rend();
while(first!=last && *first==0) ++first;
if(first==last) x.resize(1, 0);
else x.resize(last-first);
}
|
| Listing 8 |
Note that this function assumes that we shall be using a little-endian representation in which the most significant digits appear at the end of the vector and consequently iterates in reverse seeking the last non-zero digit. This is because, if and when in place operations increase or decrease the number of digits, we won't really want to move the least significant digits, as we would need to if we used a big-endian representation.
The constructors are fairly straightforward and are illustrated in listing 9.
bignum::bignum() : s_(positive), x_(1, 0)
{
}
bignum::bignum(const short x)
: s_(x>=0 ? positive : negative),
x_(abs(x))
{
}
bignum::bignum(const unsigned short x)
: s_(positive), x_(1, x)
{
}
bignum::bignum(const long x)
: s_(x>=0 ? positive : negative)
{
const unsigned long ux = labs(x);
x_.reserve(2);
x_.push_back(digit_type(ux&mask));
if(ux>mask)
x_.push_back(digit_type(ux>>shift));
}
bignum::bignum(const unsigned long x)
: s_(positive)
{
x_.reserve(2);
x_.push_back(digit_type(x&mask));
if(x>mask) x_.push_back(digit_type(x>>shift));
}
bignum::bignum(const sign_type s,
const data_type &x) : s_(s), x_(x)
{
data_strip_leading_zeros(x_);
if(x_.back()==0) s_ = positive;
}
|
| Listing 9 |
The data access functions sign and magnitude and the swap and negate member functions are similarly simple as shown in listing 10.
bignum::sign_type
bignum::sign() const
{
return s_;
}
const bignum::data_type &
bignum::magnitude() const
{
return x_;
}
void
bignum::swap(bignum &x)
{
std::swap(s_, x.s_);
std::swap(x_, x.x_);
}
bignum &
bignum::negate()
{
if(x_.back()!=0) s_ = sign(-s_);
return *this;
}
|
| Listing 10 |
The choice of a little-endian representation is also reflected in the compare function, shown in listing 11, where we use const_reverse_iterator s in the data_compare helper function to search for the most significant digit that differs in the two numbers in the event that they are the same sign and have the same number of digits.
int
data_compare(const bignum::data_type &x1,
const bignum::data_type &x2)
{
assert(x1.size()==x2.size());
bignum::data_type::const_reverse_iterator
first1 = x1.rbegin();
bignum::data_type::const_reverse_iterator
last1 = x1.rend();
bignum::data_type::const_reverse_iterator
first2 = x2.rbegin();
while(first1!=last1 && *first1==*first2)
{
++first1;
++first2;
}
if(first1==last1) return 0;
if(*first1>*first2) return 1;
return -1;
}
int
bignum::compare(const bignum &x) const
{
const int dir = s_;
if(x.s_!=s_) return dir;
if(x_.size()>x.x_.size()) return dir;
if(x_.size()<x.x_.size()) return -dir;
return data_compare(x_, x.x_) * dir;
}
|
| Listing 11 |
We shall perform addition in much the same way as we were taught to with pencil and paper when we were children. We begin with a helper function that we will use to add single digits and check whether or not we have to carry over a 1, as illustrated in listing 12.
bool
data_add(bignum::digit_type &x1,
const bignum::digit_type x2, const bool carry)
{
x1 += x2;
if(carry) ++x1;
return x1<x2 || (carry && x1==x2);
}
|
| Listing 12 |
Note that we pass in a flag to indicate whether a carry needs to be added to the digits and that we exploit the rules of unsigned arithmetic in C++ to check whether the result will itself generate a carry. Specifically, n bit unsigned arithmetic in C++ is defined as being modulo 2 n and hence any result that wraps around, and therefore generates a carry, will be less than both of the terms in the sum or, if a carry was also added, perhaps equal to one of them.
We use this in conjunction with a second helper function that adds all of the digits contained in a pair of bignum 's data_type s, as shown in listing 13.
void
data_add(bignum::data_type &x1,
const bignum::data_type &x2)
{
typedef bignum::data_type::iterator
iterator;
typedef bignum::data_type::const_iterator
const_iterator;
if(x1.size()<x2.size()) x1.resize(x2.size(),
0);
iterator first1 = x1.begin(),
last1 = x1.end();
const_iterator first2 = x2.begin(),
last2 = x2.end();
bool carry = false;
while(first2!=last2)
carry = data_add (*first1++,
*first2++, carry);
while(first1!=last1 && carry)
carry = data_add (*first1++, 0, carry);
if(carry) x1.push_back(1);
}
|
| Listing 13 |
We first ensure that x1 is as least as big as x2 by resizing and padding it with zeros if it is smaller.
The first loop then adds, with carry, the digits up to the last in x2 . The second loop ensures that further carries are properly added to any more significant digits of x1 . Note that our initial padding of x1 with zeros in the event that it has fewer digits than x2 ensures that we don't have to worry about dealing with reaching the end of x1 before we reach the end of x2 .
Subtraction is a little more difficult since it is not a symmetric operation. We shall therefore wish to ensure that we always subtract the smaller number from the larger and shall need to explicitly keep track of the sign of the result.
This is reflected in the first helper function, shown in listing 14.
bool
data_subtract(bignum::digit_type &y,
const bignum::digit_type x1,
const bignum::digit_type x2,
const bool carry)
{
y = x1-x2;
if(carry) --y;
return y>x1 || (carry && y==x1);
}
|
| Listing 14 |
Note that we treat the operation in much the same way as we did addition, but since we don't know which number will be the larger, can no longer perform the operation in-place.
The second helper function, illustrated in listing 15, ensures that the digits of the larger number are passed as x1 to this function and the digits of the smaller number are passed as x2 .
int
data_subtract(bignum::data_type &x1,
const bignum::data_type &x2)
{
typedef bignum::data_type::iterator
iterator;
typedef bignum::data_type::const_iterator
const_iterator;
const int dir = data_compare(x1, x2);
if(x1.size()<x2.size())
x1.resize(x2.size(), 0);
const_iterator first1 =
(dir>=0) ? const_iterator(x1.begin())
: x2.begin();
const_iterator last1 =
(dir>=0) ? const_iterator(x1.end())
: x2.end();
const_iterator first2 =
(dir>=0) ? x2.begin()
: const_iterator(x1.begin());
const_iterator last2 =
(dir>=0) ? x2.end()
: const_iterator(x1.end());
iterator out = x1.begin();
bool carry = false;
while(first2!=last2)
carry = data_subtract(*out++, *first1++,
*first2++, carry);
while(first1!=last1)
carry = data_subtract(*out++, *first1++,
0, carry);
data_strip_leading_zeros(x1);
return dir;
}
|
| Listing 15 |
Note that, since we ensure that the smaller number always is subtracted from the larger, we don't need to deal with a final carry. We do however need to ensure that we strip any leading zeros since we are using the number of digits during the comparison operation. Finally, we must also return the sign of the result.
Now that we can add and subtract the underlying data_type we can implement addition and subtraction operators for the bignum type itself. We must take care to direct these operations to the addition and subtraction helper functions according to whether the numbers have the same sign or not, as shown in listing 16.
bignum &
bignum::operator+=(const bignum &x)
{
int dir = 1;
if(x.s_==s_) data_add(x_, x.x_);
else dir = data_subtract(x_, x.x_);
if(dir < 0) negate();
else if(dir == 0) s_ = positive;
return *this;
}
bignum &
bignum::operator-=(const bignum &x)
{
int dir = 1;
if(x.s_==s_) dir = data_subtract(x_, x.x_);
else data_add(x_, x.x_);
if(dir < 0) negate();
else if(dir == 0) s_ = positive;
return *this;
}
|
| Listing 16 |
Irritatingly, multiplication is a little less straightforward. The scheme we were taught as children is an O ( n 2 ) operation for multiplying two n digit numbers. More efficient schemes exist but unfortunately they are much more complicated. One, for example, recasts multiplication as a discrete convolution operation and exploits the Fast Fourier Transform to compute it efficiently [ Press92 ].
bignum &
bignum::operator*=(const bignum &x)
{
data_type result(x_.size()+x.x_.size());
for(size_t i=0;i!=x_.size();++i)
{
for(size_t j=0;j!=x.x_.size();++j)
{
bool carry; size_t k;
const product_type term
= product_type(x_[i]) *
product_type(x.x_[j]);
const digit_type lo(term & mask);
const digit_type hi(term >> shift);
carry = data_add(result[i+j], lo, false);
for(k=1;carry;++k) carry =
data_add(result[i+j+k], 0, carry);
carry = data_add(result[i+j+1], hi, false);
for(k=2;carry;++k) carry =
data_add(result[i+j+k], 0, carry);
}
}
data_strip_leading_zeros(result);
if(s_==x.s_ || result.back()==0) s_ = positive;
else s_ = negative;
x_.swap(result);
return *this;
}
|
| Listing 17 |
For this treatment, the simpler, less efficient approach, as given in listing 17, will have to suffice.
We use product_type values during the multiplication of terms so that we can represent numbers that would overflow digit_type . Note that since we are assuming that the former is exactly twice as wide as the latter it is guaranteed to be large enough to represent any such product.
Similarly, we can be certain that the product will have no more digits than the sum of those in its terms, and hence do not need to check whether we are accessing the result within its bounds whilst accumulating carries.
Note that the sign of the result is positive if both terms have the same sign or if the result is zero and is negative otherwise. Checking that the leading digit is zero is sufficient for the latter since zero is the only number for which we allow one.
A further irritation is that fact that division is more difficult still. Once again we shall use the simple but inefficient scheme we learnt as children rather than the efficient but complicated schemes that we should want to use for any real-world implementation.
Specifically, we shall implement long division.
As it turns out, long division is algorithmically simplest in binary. This is chiefly due to the fact that in binary we only need to find how far to the left we can shift the number we are dividing and still be smaller than the current remainder, rather than guess at what multiple of it and the current power of 10 can be subtracted from the remainder.
For example, consider dividing 4735 by 68.
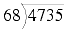
At first glance it might appear that there could be a 7 in the tens column, but on closer inspection we find it must be a 6, yielding

It's reasonably obvious that there must be a 9 in the units column, giving us
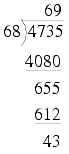
Performing the same division in binary requires more steps, but at none of them do we need to guess at the multiplicative factor that we shall place in each column; it is self-evident whether it should be a 0 or a 1.
Using the same example, but in binary, we have
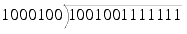
This first step in the calculation is trivially
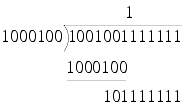
since this is largest shift which leaves a positive remainder.
Similarly, the remaining steps are

giving us again a result of 69 and a remainder of 43, but this time using nothing but shift, compare and subtraction operations.
The first thing we shall need is a helper function to perform the shift operation, given in listing 18.
void
data_shift(bignum::data_type &y,
const bignum::data_type &x,
const size_t shift, const size_t bits)
{
assert(!x.empty() && x.back()!=0);
const size_t digits = (
shift+bits+bignum::shift-1)/bignum::shift;
y.assign(digits, 0);
const size_t major = shift / bignum::shift;
const size_t minor = shift % bignum::shift;
for(size_t i=0;i!=x.size();++i)
{
const size_t lo = x[i]<<minor;
const size_t hi = x[i]>>(
bignum::shift-minor);
y[i+major] |= lo;
if(hi!=0) y[i+major+1] |= hi;
}
}
|
| Listing 18 |
The next thing we need is a function to calculate the number of significant bits, as shown in listing 19. Note that, once again, we are relying upon the fact that we do not allow leading zeros except for zero itself which consists of a single digit and also that the underlying representation must consequently have at least 1 digit.
size_t
data_bits(const bignum::data_type &x)
{
assert(!x.empty());
size_t n = (x.size()-1)*bignum::bits;
bignum::digit_type digit = x.back();
while(digit)
{
digit >>= 1;
++n;
}
return n;
}
|
| Listing 19 |
The implementation of division is fairly straightforward, as the description of binary long division suggests. Once again we shall use a helper function since we can calculate both the result of the division and the remainder at the same time, which may prove useful. Its implementation is given in listing 20.
bignum::data_type
data_divide(bignum::data_type &x1,
const bignum::data_type &x2)
{
if(x2.back()==0)
throw std::invalid_argument("");
const size_t bits2 = data_bits(x2);
bignum::data_type y;
bignum::data_type result(x1.size(), 0);
while(data_compare(x1, x2)>=0)
{
const size_t bits1 = data_bits(x1);
size_t shift = bits1-bits2;
assert(shift>0 || data_compare(x1, x2)==0);
data_shift(y, x2, shift, bits2);
if(data_compare(x1, y)<0)
data_shift(y, x2, --shift, bits2);
data_subtract(x1, y);
const size_t major = shift / bignum::shift;
const size_t minor = shift % bignum::mask;
result[major] |= 1U<<minor;
}
data_strip_leading_zeros(result);
return result;
}
|
| Listing 20 |
Note that the original value is replaced by the remainder and the result is returned.
Furthermore it is necessary to check whether the divisor is zero since the main loop will never terminate if it is.
Since all of the work is being done in the helper function, the division operator is fairly simple, as shown in listing 21.
bignum &
bignum::operator/=(const bignum &x)
{
x_ = data_divide(x_, x.x_);
if(s_==x.s_ || x_.back()==0) s_ = positive;
else s_ = negative;
return *this;
}
|
| Listing 21 |
Arbitrary precision fixed point
Using our arbitrary precision integer type as the underlying representation for a fixed point type, we can trivially solve the problem of overflow. If we are only performing additive operations on numbers that are sure to be representable with some specific number of decimal places, then we are set.
Unfortunately it does nothing to solve the problems of truncation error, cancellation error or order of execution; as a case in point consider 1/3.
In addition it is not particularly efficient in time or space; to represent the maximum double precision IEEE value would take 128 bytes, as opposed to 8 for the former.
So, unfortunately, arbitrary precision fixed point also seems to be something of a lame duck as far as general purpose arithmetic is concerned.
Quack quack.
References and further reading
[Press92] Press et al, Numerical Recipes in C (2nd ed.), Cambridge University Press, 1992.











