Can AI replace programmers? Frances Buontempo demonstrates how to autogenerate code and why we may not be replaceable yet.
Programming is difficult. Since the dawn of computers, various attempts have been made to make programmers’ lives easier. Initially, programming involved low level work, which we would struggle to recognize as a language in any way, shape or form. In order to ease the situation, automatic programming was introduced. This may sound as though programmers could be automated away; however, at the time this meant high level languages. Biermann [Biermann76] begins his introduction by saying:
Ever since the early days of electronic computers, man has been using his ingenuity to save himself from the chores of programming. Hand coding in machine language gave way to assembly language programming, which was replaced for most users by compiled languages.
He goes on to ask how much could be automatically generated, for example could input/output specification allow automatic generation of the code in-between? This question raises its head from time to time.
In this article, I will illustrate one approach, mentioning the difficulties involved and considering if it can become widespread. Before we begin, bear in mind Biermann was writing at a time when high level programming languages were cutting edge. Prior to these, programmers coded numerical operations using absolute addresses, hexadecimal programming if you will. The introduction of assembly languages was the start of the high level language evolution. The next step removed programmers further from the machine, introducing computers that programmed themselves, in some sense. “Interpreters, assemblers, compilers, and generators—programs designed to operate on or produce other programs, that is, automatic programming” according to Mildred Koss [Wikipedia]. It could be argued that we no longer program computers. Instead, we give high level instructions, and they write the code for us. Computers still need our input in this model though. Though automatic programming is what we might now simply call programming, another approach to programming, alluded to by Biermann’s mention of code generation from specification, known as Program Synthesis has received attention again recently. In particular Microsoft have been writing about the subject. According to Microsoft [Microsoft17a]:
Program synthesis is the task of automatically finding a program in the underlying programming language that satisfies the user intent expressed in the form of some specification. Since the inception of AI in the 1950s, this problem has been considered the holy grail of Computer Science.
Their paper [Microsoft17b] offers a literature review covering common program synthesis techniques and potential future work in the field. One topic they mention is Genetic Programming. My article will provide you with an introduction to this technique, using the time honoured FizzBuzz problem.
According to the c2 wiki [c2], FizzBuzz is an interview question, “designed to help filter out the 99.5% of programming job candidates who can't seem to program their way out of a wet paper bag.”
The problem is as follows:
Write a program that prints the numbers from 1 to 100. But for multiples of three print “Fizz” instead of the number and for the multiples of five print “Buzz”. For numbers which are multiples of both three and five print “FizzBuzz”.
Genetic programming (GP) starts from a high-level statement of ‘what needs to be done’ and automatically creates a computer program to solve the problem. In this sense, is it identical to other synthesis techniques. GP falls into a broader area of stochastic search, meaning the search is partly random. In theory, a completely randomly generated program may solve the problem at hand, but genetic programing uses the specification, or in simpler language, tests, to guide the search. GP works in a similar manner to a genetic algorithm. I previously gave a step by step guide to coding your way out of a paper bag, regardless of whether or not it was wet, in Overload [Buontempo13], and my book [Buontempo19] goes into more detail.
A basic genetic algorithm finds variables that solve a problem, either exactly or approximately. In practice this means a set of tests must be designed up front, also known as a fitness or cost function to ascertain whether the problem has been solved. A potential solution is assessed by running the tests with the chosen variables and using the outcome as a score. This could be number of tests passed, a cost which could be in dollars to be minimised or a ‘fitness’ to be maximized, such as money saved. The potential applications are broad, but the general idea of a test providing a numerical score to be maximized or minimized means a genetic algorithm can also be seen as an optimization technique. Genetic algorithms are inspired by the idea of Darwinian evolution, forming a subset of evolutionary algorithms. They use selection and mutation to drive the population towards greater fitness, inspired by the idea of the survival of the fittest.
The algorithm starts with a collection of fixed length lists populated at random. The values can be numbers, Booleans or characters, to investigate problems requiring numerical solutions, various constraint-based problems, hardware design and much more besides. They can even be strings, such as place names, allowing a trip itinerary to be discovered. The problem at hand will steer the size of the list. Some problems can be encoded in various ways, but many have one obvious encoding. If you want to discover two numbers, your list will comprise two numbers. The number of solutions, or population size, can be anything. Starting small and seeing what happens often works, since this will progress quickly, but may get stuck on bad solutions. The fixed length lists are often referred to as genotypes, alluding to genes representing a chromosome. The solutions can be assessed, or tested, and the best solution reported. The average, best, worst and standard deviation of scores can also help decide how well the search is progressing. As the algorithm continues, the score should improve. At its simplest the population will remain fixed size over the duration of the search, though variations allow it to grow or shrink. At each step, the population can be completely or partially replaced by creating or ‘breeding’ new lists from ‘better’ solutions or ‘parents’. The parent solutions are taken from the population, using one of many selection algorithms. A tournament selection is the simplest to implement and understand. A fixed number are randomly selected from the population and the two with the optimal score are selected. This fixed number is another decision that must be made. It could vary over the life of the algorithm.
Once two parents are selected, they ‘breed’, referred to as ‘crossover’ or recombination. For a list of two variables, this could be achieved by splitting the variables in half, passing one value (or gene) from each parent to the new offspring (Figure 1)
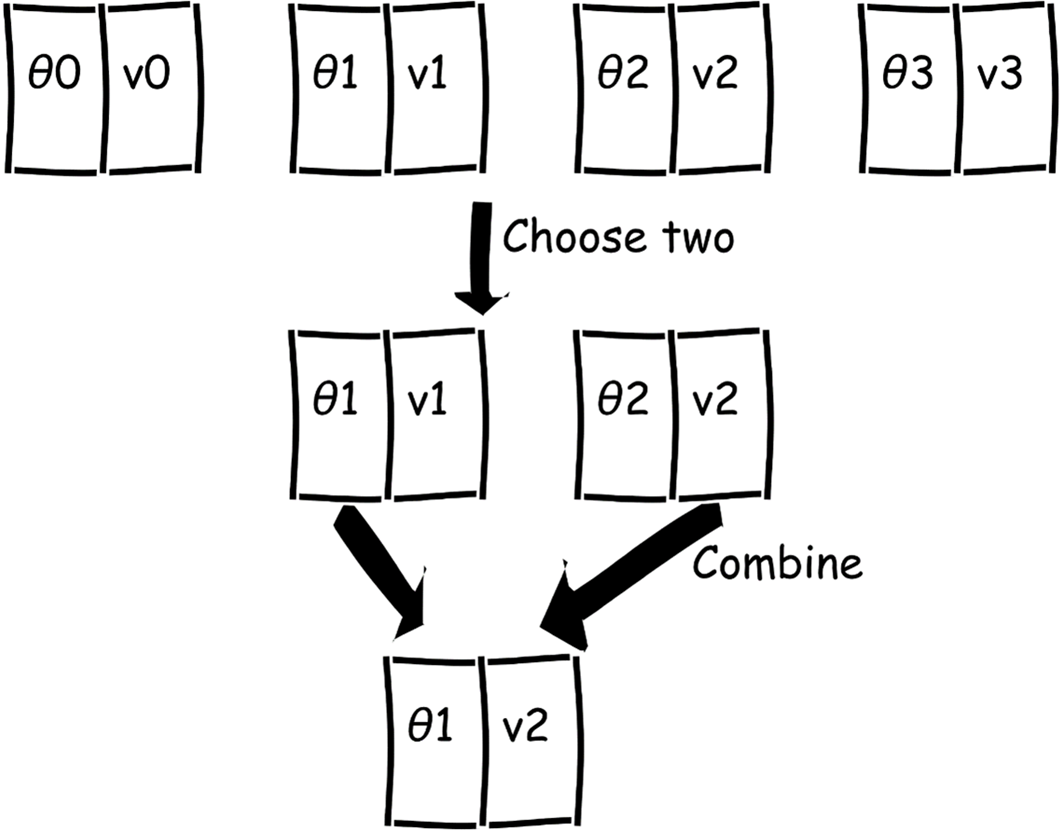 |
| Figure 1 |
For more than two variables, there are many other options: splitting at a random point, splitting in various places and interleaving the genes, alternating, and so on. Regardless of the crossover strategy, this alludes to a population gene pool with gene crossover forming new offspring. Survival of the fittest, or fit enough, ensures better adapted genes survive.
Crossover will explore the search space of potential solutions, though may miss some. In order to avoid getting stuck in a rut, mutation is also used, again alluding to natural selection. A random percentage of the new solutions are mutated. This percentage is yet another variable, or hyper-parameter to choose. In effect, this means flipping a Boolean value, incrementing, decrementing or scaling a number, or replacing a value with an entirely new random value. The combination of selection, pushing solutions to get better, along with crossover and mutation encourages exploration of the search space. This is useful if a brute force solution would take too long, since it explores fruitful looking parts of the space without needing to try everything. The algorithm is not guaranteed to work, but even if it cannot solve your problem the evolved attempts at a solution will reveal details about the shape of the search and solution space.
It should be noted that crossover and mutation can generate invalid solutions. A trip itinerary could end up with the same place twice while leaving somewhere out. A numerical problem may end up with negative numbers which are inappropriate. Such unviable solutions could be killed immediately, however the testing, or fitness step will also weed them out, if designed appropriately. This is one of many decisions to be made.
Once the population has been fully or partially replaced, using crossover and mutation, the algorithm’s progress is reported, again by best, along with any other statistics required. The breed → test → report cycle is repeated either for a pre-specified number of times or until a good enough solution is found. Recall that several hyper-parameters had to be chosen – rates of mutation, how to select parents, how big a population size, how to perform crossover. A genetic algorithm may be run several times with different hyper-parameters before a solution is found.
With one change, from solutions as lists to solutions as trees, we can switch from a genetic algorithm to genetic programming. The tree can represent a program, either as an expression or an abstract syntax tree. GP also uses crossover, mutation and testing to explore the search space. Aside from hyper-parameter choice, which is admittedly difficult, a suite of tests to pass means GP can generate code for us. I shall take the liberty of borrowing Kevlin Henney’s FizzBuzz test suite. They comprise eight tests, which are necessary and sufficient for FizzBuzz, as follows:
- Every result is ‘Fizz’, ‘Buzz’ ‘FizzBuzz’ or a decimal string
- Every decimal result corresponds to its ordinal position
- Every third result contains ‘Fizz’
- Every fifth result contains ‘Buzz’
- Every fifteenth result is ‘FizzBuzz’
- The ordinal position of every ‘Fizz’ result is divisible by 3
- The ordinal position of every ‘Buzz’ is divisible by 5
- The ordinal position of ‘FizzBuzz’ is divisible by 15
These form our fitness function, giving a maximum score of eight. A score of minus one will be awarded to programs which are not viable (for example, invalid syntax or a run time error).
In what follows, I shall use the Distributed Evolutionary Algorithms in Python (DEAP) framework [DEAP-1]. Other frameworks are available. First, a Toolbox object is required. This will hold all the parts we need.
toolbox = base.Toolbox()
Of note, DEAP does not use an abstract syntax tree directly, instead what are described as primitive operators are required, stored in a ‘primitive set’.
primitive_set = gp.PrimitiveSet("MAIN", 1)
This requires some extra boilerplate to add primitives (operators and functions) to the set, such as operator.add and similar. In addition you can add terminals (leaf nodes in a tree), such as 3 or ‘Fizz’. You can also add what are termed ephemeral constants, which could take a lambda that returns a random number. This allows constants to be generated per solution.
The full code listing is available in a gist [Buontempo], but Listing 1 contains a few examples I used.
primitive_set.addPrimitive(operator.and_, 2)
primitive_set.addPrimitive(operator.or_, 2)
primitive_set.addPrimitive(if_then_else, 3)
primitive_set.addPrimitive(mod3, 1)
primitive_set.addPrimitive(mod5, 1)
primitive_set.addPrimitive(mod15, 1)
primitive_set.addTerminal("Buzz")
primitive_set.addTerminal("Fizz")
primitive_set.addTerminal("FizzBuzz")
|
| Listing 1 |
The mysterious if_then_else is defined as follows:
def if_then_else(x,y,z):
if x:
return y
else:
return z
There may be a neater way to get DEAP to use this construct, but it will do.
The modXXX functions are again a bit of a hack, for example:
def mod3(x):
return operator.mod(x, 3) == 0
A primitive takes a callable and the number of parameters, while a terminal, or leaf node, takes a value only. I did not manage to get the GP to find the values 3, 5 or 15 which was disappointing. The gist includes a version to generate code finding if a number is odd or even, using new primitives and ‘constants’:
primitive_set.addPrimitive(operator.mod, 2)
primitive_set.addEphemeralConstant("rand101",
lambda: random.randint(-1,1))
primitive_set.addEphemeralConstant("randints",
lambda: random.randint(0,10))
This did work, so in theory I suspect the GP could discover more of the parts needed for FizzBuzz with more experimentation. For this article, we shall cheat and give the GP some help.
It is worth naming the arguments so the generated code looks less ugly:
primitive_set.renameArguments(ARG0='x')
Once the primitive set is populated, DEAP can form an expression:
expr = gp.genFull(primitive_set, min_=1, max_=3)
that can then be converted to tree:
tree = PrimitiveTree(expr)
Printing the randomly generated tree gives
mod3('Fizz')
You can ‘compile’ this to see what happens as follows:
example = toolbox.compile(tree)
This returns a lambda, which you can then call. The astute amongst you may notice this will lead to a run time error. Not all expressions randomly generated are valid. Invalid trees can be dropped immediately.
In order to run the algorithm, we tell DEAP how to assess the fitness of individual trees
creator.create("FitnessMax", base.Fitness,
weights=(1.0,))
creator.create("Individual", gp.PrimitiveTree,
fitness=creator.FitnessMax)
This is very stringly typed, but allows much flexibility. The weights for the fitness are set to one, meaning the number of tests passed, from our eight tests, is multiplied by one. Setting the weight to -1 would seek out a minimum rather than a maximum. The primitive tree type is “specifically formatted for optimization of genetic programming operations” according to the documentation [DEAP-2]. In theory you could extend this or make a new type. A strongly typed version is available. We will stick to the PrimitiveTree type for this example.
Using the toolbox we created earlier, we register expressions, individuals, populations and a compile function (see Listing 2).
toolbox.register("expr", gp.genHalfAndHalf,
primitive_set=primitive_set, min_=1, max_=2)
toolbox.register("individual", tools.initIterate,
creator.Individual, toolbox.expr)
toolbox.register("population", tools.initRepeat,
list, toolbox.individual)
toolbox.register("compile", gp.compile,
primitive_set=primitive_set)
|
| Listing 2 |
The half and half for the expressions means half the time expressions are generated with grow (between the maximum and minimum height) and the other half with full (maximum height). Letting expressions get too big takes time and may not give much benefit. In theory you could add if true inside if true many, many times. Without baking preferences for acceptable source code, this will have no impact on the fitness of a solution, but take time to grow, so the maximum tree size parameters can help.
I initially tried 5 and the trees improved but then stuck below 100% fitness, then started getting worse. As with genetic algorithms, and almost all machine learning, you need to experiment with the parameters.
We need to register a few more things then we’re ready to go. We need a fitness function (Listing 3).
def tests_passed (func, points):
passed = 0
def safe_run(func, x):
try:
return func(x)
except:
return -1
results = [safe_run(func, x) for x in points]
# not listed for brevity,
# but passed += 1 for each of the eight tests
# assessed on the results list just formed
return passed
def fitness(individual, points):
# Transform the tree expression in a callable
# function
func = toolbox.compile(expr=individual)
return tests_passed(func, points),
|
| Listing 3 |
Yes, the fitness function returns a tuple, required by the framework, so that is not a spare comma at the end. The tests_passed function takes the function generated by GP and runs it over some numbers, conventionally 1 to 100 for FizzBuzz, though I have chosen to start at zero. safe_run is used to catch and penalize errors.
We then register this fitness function and set up more options and parameters (see Listing 4).
toolbox.register("evaluate",
fitness points=range(101))
toolbox.register("select", tools.selTournament,
tournsize=3)
toolbox.register("mate", gp.cxOnePoint)
toolbox.register("expr_mut", gp.genFull, min_=0,
max_=2)
toolbox.register("mutate", gp.mutUniform,
expr=toolbox.expr_mut, pset=primitive_set)
|
| Listing 4 |
I also added some statistics to the toolbox to track the algorithm's progress. This used DEAP’s multi-statistics tool (again, full details in the gist)
mstats = tools.MultiStatistics(…)
These are reported at each step in the loop. To keep track of the best tree use the hall of fame:
hof = tools.HallOfFame(1)
Recall that the GP uses randomness to find solutions, so I clamped the seed for repeatable experiments, random.seed(318)
We finally decide a population size, how often to crossover and mutate, and how many generations to run this for. It’s worth trying a small population first, 10 or so, and a few generations to see what happens, then increase these if things do seem to improve over the generations:
pop = toolbox.population(n=4000)
pCrossover = 0.75
pMutation = 0.5
nGen = 75
pop, log = algorithms.eaSimple(pop, toolbox,
pCrossover, pMutation, nGen, stats=mstats,
halloffame=hof, verbose=True)
After running for several minutes we obtain an expression that generates FizzBuzz for us (Listing 5). The best tree has 81 nodes, with the expression shown in Listing 6. (See also Figure 2.)
['FizzBuzz', 1, 2, 'Fizz', 4, 'Buzz', 'Fizz', 7, 8, 'Fizz', 'Buzz', 11, 'Fizz', 13, 14, 'FizzBuzz', 16, 17, 'Fizz', 19, 'Buzz', 'Fizz', 22, 23, 'Fizz', 'Buzz', 26, 'Fizz', 28, 29, 'FizzBuzz', 31, 32, 'Fizz', 34, 'Buzz', 'Fizz', 37, 38, 'Fizz', 'Buzz', 41, 'Fizz', 43, 44, 'FizzBuzz', 46, 47, 'Fizz', 49, 'Buzz', 'Fizz', 52, 53, 'Fizz', 'Buzz', 56, 'Fizz', 58, 59, 'FizzBuzz', 61, 62, 'Fizz', 64, 'Buzz', 'Fizz', 67, 68, 'Fizz', 'Buzz', 71, 'Fizz', 73, 74, 'FizzBuzz', 76, 77, 'Fizz', 79, 'Buzz', 'Fizz', 82, 83, 'Fizz', 'Buzz', 86, 'Fizz', 88, 89, 'FizzBuzz', 91, 92, 'Fizz', 94, 'Buzz', 'Fizz', 97, 98, 'Fizz', 'Buzz'] |
| Listing 5 |
if_then_else(mod15(if_then_else(if_then_else(mul(x, 'FizzBuzz'), 'Fizz', 'Buzz'), x, if_then_else('Buzz', 'FizzBuzz', mod3(x)))), 'FizzBuzz', if_then_else(both(if_then_else(if_then_else(mod15(x), either('FizzBuzz', 'FizzBuzz'), 'FizzBuzz'), if_then_else('FizzBuzz', mod15(mod5(x)), 'Buzz'), 'Buzz'), if_then_else('Fizz', 'Buzz', if_then_else('FizzBuzz', if_then_else(if_then_else('Buzz', if_then_else(if_then_else(mod3(x), x, 'FizzBuzz'), if_then_else(x, x, either('Buzz', 'Buzz')), x), 'Fizz'), 'Fizz', x), if_then_else(either(if_then_else(x, x, mod3(x)), 'FizzBuzz'), 'Fizz', 'Fizz')))), if_then_else(mod15(x), either('FizzBuzz', either('Buzz', x)), if_then_else(mod3(x), 'Fizz', x)), 'Buzz'))
|
| Listing 6 |
| Figure 2 |
The generated expression is very unpleasant, but it works. In my defence, I recently came across a report into ‘Modified Condition Decision Coverage’ to “assist with the assessment of the adequacy of the requirements-based testing process”. [US-FAA]. On page 177, the authors cite an expression with 76 conditionals found in Ada source code for aeroplane black boxes (Listing 7).
Bv or (Ev /= El) or Bv2 or Bv3 or Bv4 or Bv5 or Bv6 or Bv7 or Bv8 or Bv9 or Bv10 or Bv11 or Bv12 or Bv13 or Bv14 or Bv15 or Bv16 or Bv17 or Bv18 or Bv19 or Bv20 or Bv21 or Bv22 or Bv23 or Bv24 or Bv25 or Bv26 or Bv27 or Bv28 or Bv29 or Bv30 or Bv31 or Bv32 or Bv33 or Bv34 or Bv35 or Bv36 or Bv37 or Bv38 or Bv39 or Bv40 or Bv41 or Bv42 or Bv43 or Bv44 or Bv45 or Bv46 or Bv47 or Bv48 or Bv49 or Bv50 or Bv51 or (Ev2 = El2) or ((Ev3 = El2) and (Sav /= Sac)) or Bv52 or Bv53 or Bv54 or Bv55 or Bv56 or Bv57 or Bv58 or Bv59 or Bv60 or Bv61 or Bv62 or Bv63 or Bv64 or Bv65 or Ev4 /= El3 or Ev5 = El4 or Ev6 = El4 or Ev7 = El4 or Ev8 = El4 or Ev9 = El4 or Ev10 = El4 |
| Listing 7 |
So, humans can write complicated code too. Somewhere in the middle of the figure you may see the conditional
if FizzBuzz or FizzBuzz: then FizzBuzz
It is possible to prune a tree, however if the aim of program synthesis is to remove programmer from the process, no one need ever see the implementation.
It took considerably longer to get my computer to generate this code than it would have taken to write this by hand. Any machine learning algorithm needs several runs and many attempts to tune parameters. Tools are gradually coming to the fore to track the training process. For example, Feature stores to keep cleansed data for training are becoming popular and DevMLOps is becoming a common phrase. MLFLow [MLFLow] offers a way to track training and parameter choice. Furthermore automatic parameter tuning is being investigated, for example AWS’ automatic model tuning in SageMaker [Amazon].
Was this GP FizzBuzz exercise worth the time spent? The exercise was interesting, and I encourage you to try it out. If you can get a version working without cheating, so that your computer discovers the magic numbers 3 and 5, do write in. Having an understanding of the implementation and details behind buzz words such as Artificial Intelligence is always useful.
I mentioned a Microsoft paper at the start. Program synthesis seems to be an area of research that has recently become active again. They mention a Python Programming Puzzles project “which can be used to teach and evaluate an AI’s programming proficiency” [Microsoft-1]. FizzBuzz isn’t here, yet. For further background on genetic programming, go to Genetic Programming Inc [GP] and the Royal Society Paper, ‘Program synthesis: challenges and opportunities’ [David17] gives a thorough overview . The ACM SIGPLAN published a blog giving an overview of the state of the art in 2019 [Bornholt19]. This includes Excel’s ‘Flash Fill’ [Microsoft-2], which offers suggestions to fill cells as you type based on patterns it finds. This uses an inductive approach, which you could describe as extrapolating from examples, rather than the pre-specified criteria tests approach used in this article. Program synthesis has been used to automatically derive compiler optimizations. In particular, Souper can help identify missing peephole optimizations in LLVM’s midend optimizers [Souper]. Even if computers never fully program themselves, program synthesis can be and is used for practical applications. Watch this space.
References
[Amazon] ‘How Hyperparameter Tuning Works’, availble at:https://docs.aws.amazon.com/sagemaker/latest/dg/automatic-model-tuning-how-it-works.html
[Biermann76] Biermann (1976) ‘Approaches to automatic programming’ in Advances in Computers Vol 15, p1–63, available at: https://www.sciencedirect.com/science/article/pii/S0065245808605197
[Bornholt19] James Bornholt (2019) ‘Program Synthesis in 2019’, available at https://blog.sigplan.org/2019/07/31/program-synthesis-in-2019/
[Buontempo] GP FizzBuzz: https://gist.github.com/doctorlove/be4ebe4929855f69861c13b57dbcf3aa
[Buontempo13] Frances Buontempo (2013) ‘How to Program Your Way Out of a Paper Bag Using Genetic Algorithms’ in Overload 118, available from https://accu.org/journals/overload/21/118/overload118.pdf#page=8
[Buontempo19] Frances Buontempo (2019) Genetic Algorithms and Machine Learning for Programmers, The Pragmatic Bookshelf, ISBN 9781680506204. See https://pragprog.com/titles/fbmach/genetic-algorithms-and-machine-learning-for-programmers/
[c2] ‘Fizz Buzz Test’ on the c2 wiki: https://wiki.c2.com/?FizzBuzzTest
[David17] Cristina David and Daniel Kroening (2017) ‘Program synthesis: challenges and opportunities’, The Royal Society September 2017, available at: https://royalsocietypublishing.org/doi/10.1098/rsta.2015.0403
[DEAP-1] DEAP documentation: https://deap.readthedocs.io/en/master/
[DEAP-2] Genetic Programming: https://deap.readthedocs.io/en/master/api/gp.html
[GP] Genetic http://www.genetic-programming.com/
[Microsoft-1] https://github.com/microsoft/PythonProgrammingPuzzles
[Microsoft-2] Excel’s ‘Flash Fill’: https://support.microsoft.com/en-us/office/using-flash-fill-in-excel-3f9bcf1e-db93-4890-94a0-1578341f73f7
[Microsoft17a] ‘Program Synthesis’ abstract (2017) https://www.microsoft.com/en-us/research/publication/program-synthesis/
[Microsoft17b] ‘Program Synthesis’ paper (2017) https://www.microsoft.com/en-us/research/wp-content/uploads/2017/10/program_synthesis_now.pdf
[MLFLow] https://mlflow.org/
[Souper] https://github.com/google/souper
[US-FAA] Federal Aviation Administration (2001) ‘An Investigation of Three Forms of the Modified Condition Decision Coverage (MCDC) Criterion’, U.S. Department of Transportation, available from:http://www.tc.faa.gov/its/worldpac/techrpt/ar01-18.pdf
[Wikipedia] Mildred Koss, quoted by Wikipedia:https://en.wikipedia.org/wiki/Automatic_programming
has a BA in Maths + Philosophy, an MSc in Pure Maths and a PhD technically in Chemical Engineering, but mainly programming and learning about AI and data mining. She has been a programmer since the 90s, and learnt to program by reading the manual for her Dad’s BBC model B machine.












